You may complete the following entirely in a Jupyter notebook. Ensure that the notebook has your name on it. Save the notebook as a PDF and submit the PDF through Canvas.
Problem 1: Exploring the Penalty Term Hyperparameter
Evaluating impact of the C parameter on a SVM model.
- Load the wine data set from scikit learn.
- Relabel the response variable so that class 2 becomes class 1 and classes 0 and 1 become class 0. You saw something similar in Lab 2 with the Setosa/Not Setosa classes in the Iris dataset.
- Train SVM models with a linear kernel and C values of [1,10,100,1000] on the
hueandflavanoidsfeatures using theSVCclass. (Features 10 and 6, respectively.) - Plot the decision boundary, margins, and support vectors for each model. Describe how the decision boundary, margins, and support vectors change with the different values of C.
For a linear SVM, you would generally use the LinearSVC class, but use the more flexible SVC here since it allows easy access to the support vectors.
Problem 2: The Problem with Kernels
- 1-D example
- Load the dataset
kernel_problem_1.csv. Rows are observations, the first column refers to $x_{1}$ features, and the second column is given class ($y$). - Plot the observations (note: we have seen observations described by 2 features so far, but that is not always the case. Observations could be described by a single feature). Are these features linearly separable?
- Give the hyperplane that will divide this space by the given classes.
- Load the dataset
- 1-D to 2-D example
- Load the dataset
kernel_problem_2.csv. Rows are observations, the first column refers to $x_{1}$ features, and the second column is given class ($y$). - Plot the observations (note: we have seen observations described by 2 features so far, but that is not always the case. Observations could be described by a single feature). Are these features linearly separable?
- Use the following function to describe these observations in 2-dimensional space: $x_{2}=x_{1}^{2}$. Plot the observations in 2-dimensional space. Are these same observations now linearly separable?
- In this higher dimensional space, use the following description of
a hyperplane and a threshold to classify the points.
- $\hat{n} = \langle 0, 1 \rangle \quad \text{and} \quad \mathbf{r_0} = (0,5)$
- $y = \begin{cases} 0 & \text{if } f(x) < 0 \ 1 & \text{if } f(x) \geq 1 \end{cases}$
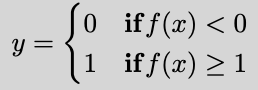
- Load the dataset
- 2-D to 3-D example
- Load the dataset
kernel_problem_3.csv. Rows are observations, the first and second columns refer to features, the third column is given class (y). - Plot the observations. Are these observations linearly separable?
- Use the following function to describe these observations in 3-dimensional
space:
- $\phi(x) = \phi \begin{bmatrix} x_1 \ x_2 \end{bmatrix} = \begin{bmatrix} x_1^2 \ \sqrt{2} x_1 x_2 \ x_2^2 \end{bmatrix}$
- Plot the observations from 3 separate perspectives - feature1 × feature2 , feature2 × feature3 , feature1 × feature3. Are these same observations now linearly separable?
- Load the dataset